Игра «Угадай задуманное число» с помощью калькулятора Windows
Игра «Угадай задуманное число» может показаться числовым фокусом. Тем не менее, она основана на определенных правилах и на двоичной системе счисления. Для упрощения отгадывания числа можно воспользоваться калькулятором Windows.
Содержание:
1. Сложение и умножение в двоичной системе счисления
2. Правила игры «Угадай задуманное число»
3. Игра начинается: последовательно делим числа пополам
4. Угадайка продолжается
5. «Угадай число» неуклонно движется к своему завершению
6. Калькулятор для программиста: как подготовиться к угадыванию числа
7. Угадываем задуманное число
8. Видео: Угадай задуманное число
9. Фокусы с разоблачениями
10. Преобразование двоичного числа в десятичное
11. О пользе троичной, четверичной и иных систем счисления
Двоичная система исчисления строится на двух цифрах: 0 и 1. Используется она обычно лишь для управления техникой: есть сигнал – это «единица», нет сигнала – это «ноль». В компьютерах на уровне «железа» прекрасно работает двоичная система. Программисты могут и умеют пользоваться двоичной системой счисления для своих непростых дел по управлению компьютерами и иной подобной техникой.
Но, оказывается, двоичная система применялась и ранее. Но не для расчетов – это сложно для применения человеком, тут нужен компьютер. А, например, для различных числовых фокусов. Да-да! Именно для фокусов с числами, чтобы поразить воображение зрителей. Одним из таких фокусов является игра «Угадай задуманное число».
Таблицы сложения и умножения в двоичной системе счисления
Иной раз удобно перевести числа из нашей привычной десятичной системы счисления с цифрами от 0 до 9 в двоичную систему с цифрами 0 и 1. Такое упрощение позволяет легко угадывать числа, а также производить различные вычисления в уме.
Ведь в двоичной системе очень простая таблица сложения:
0+0=0, 0+1=1, 1+0=0, 1+1=10.
А таблица умножения и того проще:
0*0=0, 1*0=0, 0*1=0, 1*1=1
Какие проблемы, скажем, сложить пару-тройку чисел, в которых нет ничего, кроме нулей и единиц? Но мы не будем сейчас заниматься быстрым счетом – этот навык уходит в прошлое благодаря калькуляторам и компьютерам.
Возьмем в руки калькулятор, который имеется теперь везде: в компьютерах, в телефонах, в смартфонах, в планшетах. И предложим стать участниками фокуса с точным отгадыванием числа, которое задумал второй участник игры.
Игра «Угадай задуманное число» и ее правила
Будем угадывать любые двузначные числа, используя для этого двоичную систему. Можно угадывать и трех-, четырех- и более -значные числа, только это будет дольше. А короткие числа угадывать быстрее, и потому интереснее, хотя бы для начала.
Для демонстрации фокуса нам нужен напарник, второй участник, который может быть рядом или подключиться с помощью современных средств коммуникации. Предположим, такой благодарный слушатель нашелся. Давайте предложим нашему товарищу (с калькулятором в руках!) набрать на своем калькуляторе любое двузначное число. Это число он должен запомнить, ведь мы будем его угадывать. Нам он не должен это число показывать. Мы ведь не собираемся за ним подсматривать!
Правила игры следующие. Наш партнер должен разделить задуманное число на 2, и сообщить нам, получилось ли в результате число целое, без десятичных знаков после точки, или дробное, с десятичным знаком после точки. Больше ничего он нам не должен сообщать.
Далее наш товарищ должен снова разделить полученное число на 2. Причем, если он получил от прежнего деления дробное число, то сначала он должен убрать дробную часть, чтобы делить только целое число. И снова он должен сообщить нам о том, разделилось ли число нацело или нет. И так – пока в результате на его калькуляторе не высветится «ноль».
Мы же после этого беремся угадать число, которое было на калькуляторе товарища в самом начале нашей игры в угадайку.
Игра начинается, партнер последовательно делит числа пополам
Предположим, наш товарищ по игре на своем калькуляторе набрал число 78. Мы этого не видим, и не знаем данное число. Тем не менее, оно теперь набрано на калькуляторе. Отлично! Мы же откроем обычный блокнот в компьютере или в любом другом устройстве (телефон, смартфон, айфон, планшет и прочее).
У кого нет блокнота – подойдет любой редактор, куда можно записывать символы. Да хоть обычный блокнот с карандашом или авторучкой – не обязательно на компьютере. Будем записывать только нули и единицы – ведь речь пойдет о двоичной системе счисления…
Вот как все это выглядит: на рисунке 1 показано, что слева – это наш блокнот, пока пустой, в нем ничего не записано. А справа – калькулятор нашего товарища, на котором он (она) уже успел(а) набрать загаданное число 78.
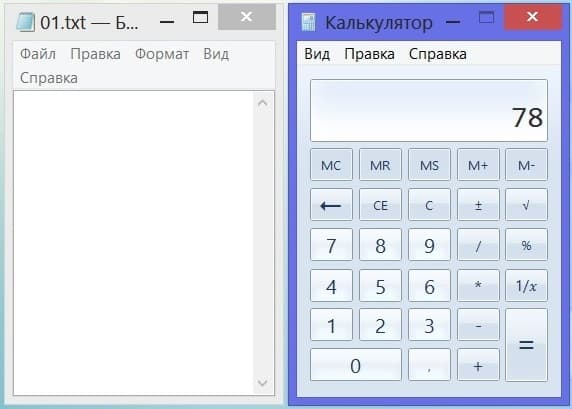
Рис. 1. Калькулятор одного игрока (справа) с загаданным числом 78 и блокнот второго игрока (слева) в игре «Угадай число».
Итак, поехали, игра «Угадай задуманное число» началась! Будем угадывать набранное число. Для начала попросим нашего товарища разделить загаданное число на 2. Это можно сделать прямо на том же калькуляторе.
Перед этим снова обратим внимание напарника на то, что он должен обязательно запомнить задуманное число! Поскольку оно сотрется с экрана калькулятора после производимых над ним арифметических действий.
Как делить число на 2 на калькуляторе
Смотрим на рисунок 2. Сначала нажимаем на знак деления «/» (на некоторых калькуляторах используется другой символ). Потом нажимаем на кнопку с цифрой 2. И, наконец, жмем на знак равенства «=».
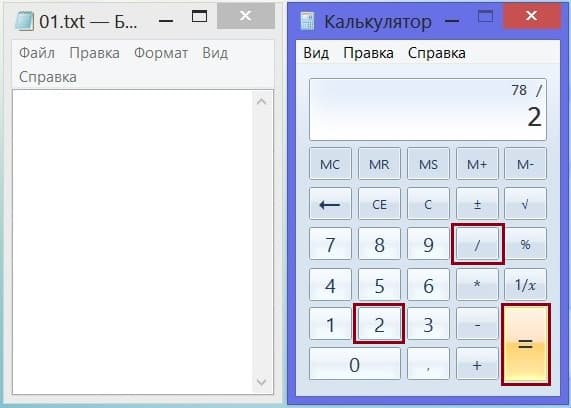
Рис. 2. Как делить число на 2 с помощью калькулятора: последовательное нажатие на кнопки «/» (делить), «2» и «=» (равно).
Результат деления задуманного числа видит наш товарищ, но мы этот результат не видим. Получилось число 39. Когда любое целое число делят на 2, может получиться либо целое число, либо дробное, у которого после точки (или запятой, как бывает на некоторых калькуляторах) будет стоять «пятерка» — пять десятых. Других вариантов деления на 2 не бывает.
Вот и мы обратим на это внимание. Попросим нашего товарища нам сообщить, какое число он получил в результате деления на 2 – целое или дробное. Он нам должен сказать не само число, которое получилось, а именно целое оно или дробное, с «пятеркой» после десятичной точки.
Как мы уже отметили, ответ получился целым – число 39. Нам сообщают, что число целое. У нас перед глазами находится блокнот. И мы в него записываем либо «единичку» (1), либо «нолик» (0):
- 1 – единицу пишем в том случае, если ответ получился дробный, с точкой и с «пятеркой» после точки
- 0 – нолик пишем тогда, когда ответ получается целый без десятичной точки.
Нам сказано, что результатом деления задуманного числа на 2 есть целое число, без десятичной точки. Значит, записываем в блокнотик одну единственную цифру «нолик» — 0 (рис. 3).
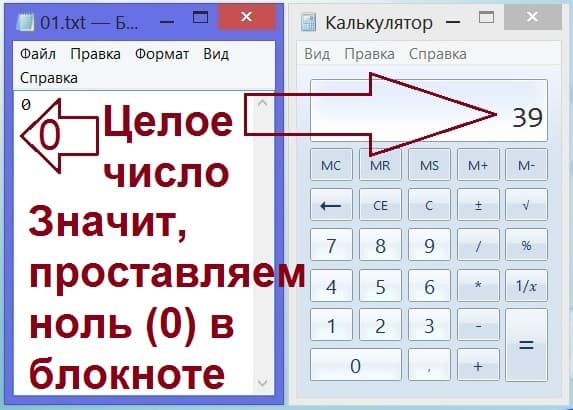
Рис. 3. Запись в блокнот (слева) первого игрока цифры «ноль» (0), если на калькуляторе (справа) второго игрока получилось целое число без десятичной точки.
Продолжаем игру с угадыванием числа
Игра «Угадай задуманное число» продолжается, еще ничего не закончилось… Наш товарищ снова делит полученный результат на 2 (напомним, что он в результате получил число 39). Ответ будет уже не целый – это 19,5. Так наш товарищ, партнер по игре «Угадай цифру» и говорит нам: «результат – не целое число».
Значит, нам надо приписать справа от только записанного «нолика» следующую цифру. То уже будет цифра 1, ведь результат – нечетный (рис. 4). У нас в блокноте теперь стоят уже две цифры: 0 и 1.
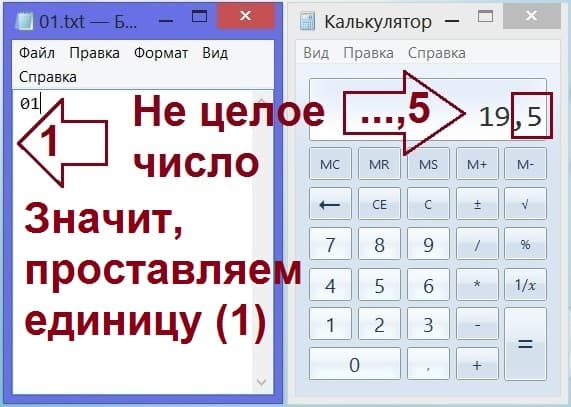
Рис. 4. Запись в блокнот (слева) первого игрока цифры «один» (1), если на калькуляторе (справа) второго игрока получилось не целое, а дробное число с десятичной точкой.
Теперь наш товарищ не может просто так разделить полученное дробное число на 2. Число сначала нужно «избавить» от дробной части. Ему (ей) придется заново набрать на калькуляторе число 19, вместо прежнего числа 19,5.
Число 19,5 не округляется! Иначе при округлении по правилам округления мы получили бы 20. Нет, нужно просто «отбросить» дробную часть, не меняя основное число. Следом нужно будет разделить это теперь уже целое число на 2 (рис. 5).
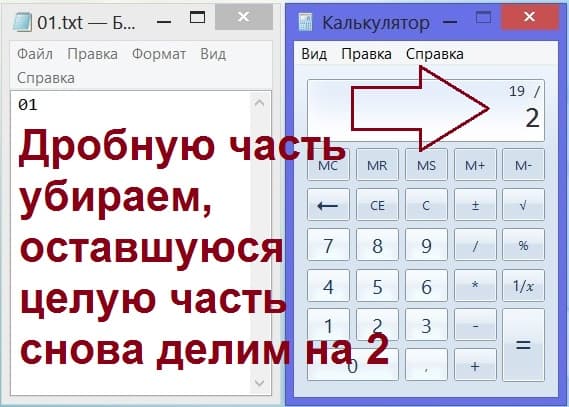
Рис. 5. Игрок «Угадай число» на калькуляторе (справа) должен отбросить дробную часть полученного не целого числа, а затем полученное целое число вновь разделить на 2.
Результатом деления 19 на 2 будет снова не целое число. Ответ – 9,5. Напарник, второй игрок сообщает итог очередного деления на 2: «Получилось не целое число». Отлично! Значит, мы приписываем к двум нашим цифрам в блокноте очередную «единичку», так как результат деления – не целое число (рис. 6).
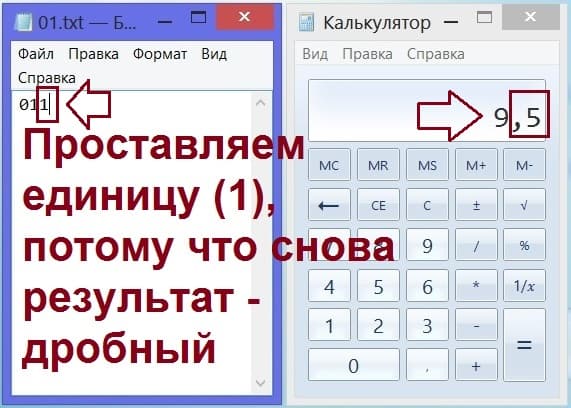
Рис. 6. В блокноте (слева) записывается очередная «единичка», поскольку на калькуляторе (справа) вновь высвечивается дробное, а не целое число.
Теперь в нашем блокноте записана последовательность из 3-х цифр: 011. А наш товарищ продолжает игру. Он «отбрасывает» запятую (точку) и «пятерку», оставляет на калькуляторе только цифру 9, и вновь делит ее пополам. Ответ – 4,5, и это не целое число. Нам сообщают итог (не целое число!), и мы приписываем следующую единичку. В нашем блокноте теперь записано 0111 (рис. 7):
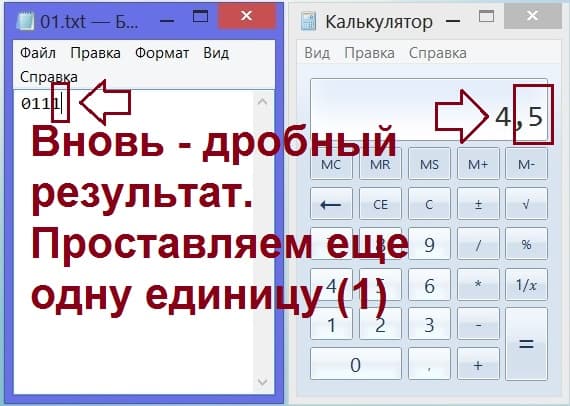
Рис. 7. Очередная «единичка» в блокноте (справа), так как на калькуляторе (слева) вновь дробное число.
Игра «Угадай задуманное число» движется к завершению
Игра приближается к своему завершению. Но еще не все числа поделены на 2. Надо отбросить «,5» и оставить только цифру 4, а затем поделить ее на 2. Ответ очевиден даже без калькулятора – это 2, то есть четное число.
Наш товарищ нам об этом говорит: «Результат деления – четное число». Услышав это, мы припишем к нашей последовательности цифр теперь уже «нолик» 0, так как результат – четное число (рис. 8). Наша последовательность стала теперь такой: 01110.
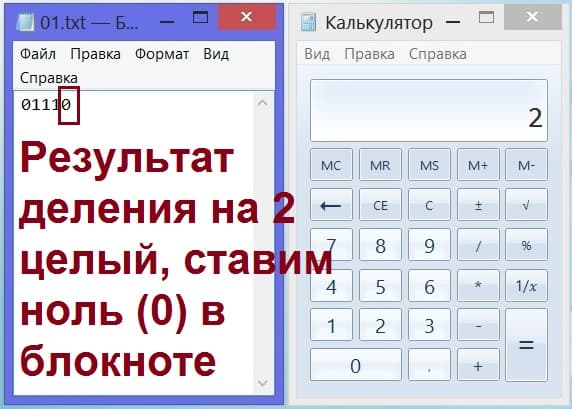
Рис. 8. Запись в блокноте (слева) очередного «нолика», так как на калькуляторе (справа) получилось целое число без десятичной точки.
Наш партнер по игре делит 2 на 2, получает 1 – это целое число, о чем нам и сообщает. Мы добавляем «нолик» к нашей записи в блокноте, и получаем последовательность 011100 (рис. 9).
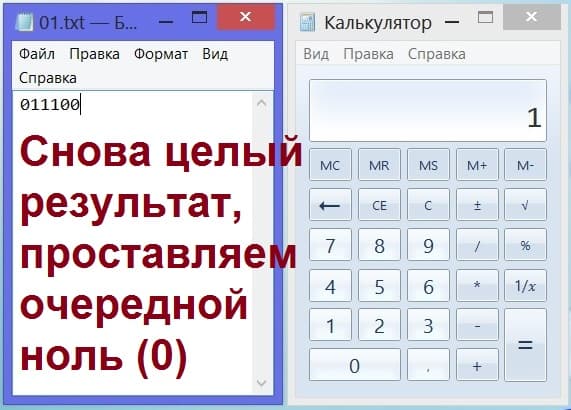
Рис. 9. Запись очередного «нуля» в блокнот (слева).
Оставшуюся одинокую «единичку» наш товарищ в очередной раз делит на 2, и получает 0,5, то есть не целое число. Признается нам в этом (что число не целое), и мы приписываем следующую единичку, получая в итоге: 0111001 (рис. 10).
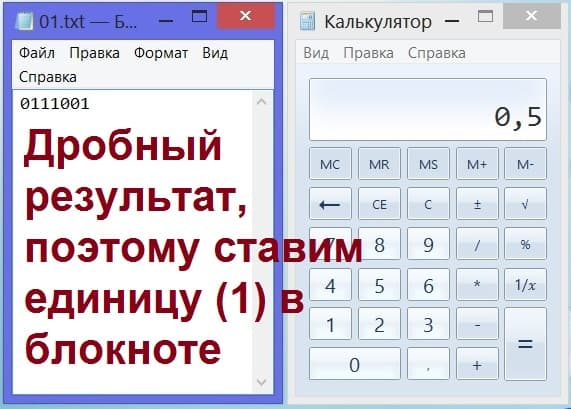
Рис. 10. Запись последней «единички» в блокноте (слева) в игре «Угадай число».
Тут наш партнер по игре убирает дробную часть числа и получает… чистый «ноль». Все, игра «Угадай задуманное число» подошла к концу! Ноль бессмысленно далее делить на что-либо. Товарищу по игре придется нам признаться, что больше он делить числа на 2 не в состоянии – на экране калькулятора высветился «ноль» (рис. 11).
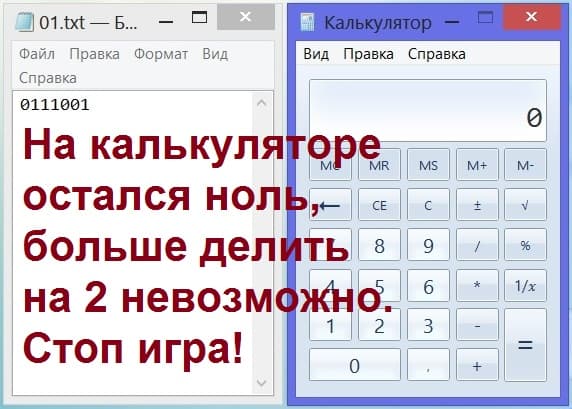
Рис. 11. Игра «Угадай число» подошла к концу активной фазы – на калькуляторе (справа) высветился чистый «ноль».
Калькулятор для программиста: готовимся угадывать задуманное число
Теперь пришло наше время угадывать число, задуманное нашим другом. Итак, перед нами последовательность нулей и единиц, записанная со слов товарища о целых или не целых числах в результате деления загаданного числа на 2 – это 0111001. Первым делом мы «разворачиваем» запись с точностью до наоборот.
Переписываем последовательность нулей и единиц с обратного конца, справа налево. Делать это надо аккуратно, чтобы не ошибиться, ничего не пропустить, ничего не заменить. Получим: 1001110 (рис. 12).
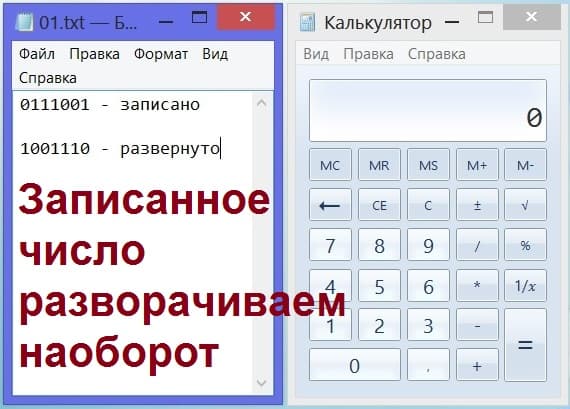
Рис. 12. Запись задом наперед полученного двоичного кода в ходе игры «Угадай задуманное число».
Вот теперь пора и нам воспользоваться калькулятором. Откроем его на нашем компьютере. Сразу после его открытия нам понадобится изменить привычный вид калькулятора, превратив его в калькулятор для программиста.
Нам понадобятся «программистские штучки» для того, чтобы угадать число. Для изменения вида калькулятора в меню «Вид» (1 на рис. 13) находим опцию «Программист» (2 на рис. 13).
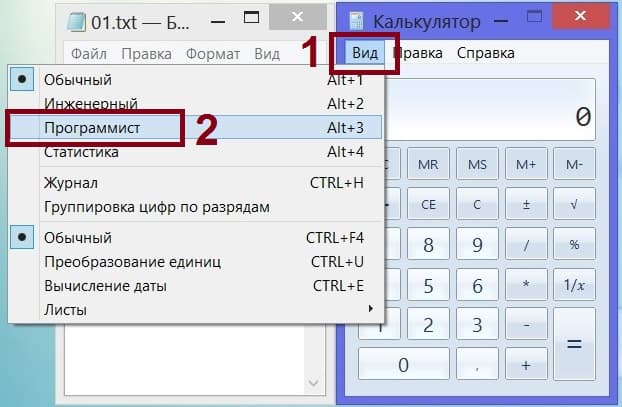
Рис. 13. Переключение компьютерного калькулятора в режим «Программист».
Далее настроим калькулятор для программиста, чтобы затем решить задачу по угадыванию числа. Отметим кнопочки настроек «Bin» (что значит «двоичный», чтобы калькулятор работал с двоичными числами) и «8 байт», чтобы калькулятор мог обрабатывать десятичные числа разрядностью до 8-и цифр. Требуемые нам настройки калькулятора для программистов продемонстрированы на рис. 14.
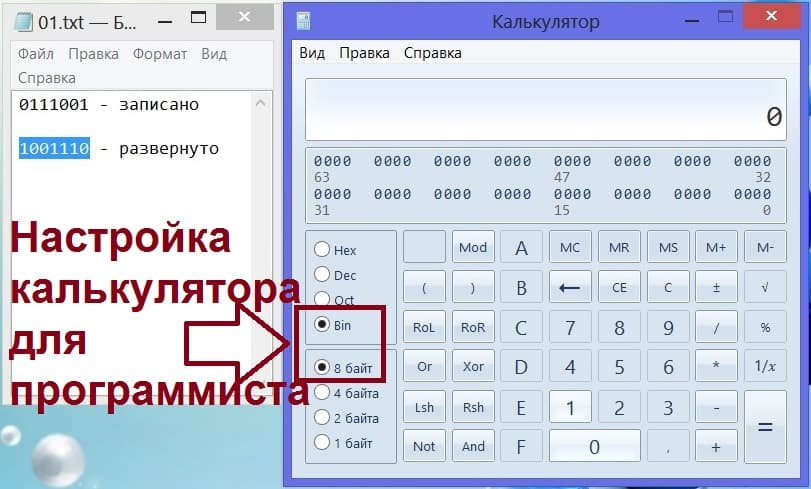
Рис. 14. Настройки калькулятора программиста для ввода и обработки двоичных чисел.
Угадываем задуманное число: калькулятор для программиста нам в помощь
Теперь осталось совсем немного. Введем перевернутое задом наперед двоичное число в калькулятор. Это можно сделать либо вручную, нажимая на единички и нолики на калькуляторе. Либо данные можно скопировать из блокнота через буфер обмена, а затем вставить их на калькуляторе из буфера обмена. В итоге на экране калькулятора мы увидим нашу перевернутую последовательность единиц и нулей: 1001110 (рис. 15).
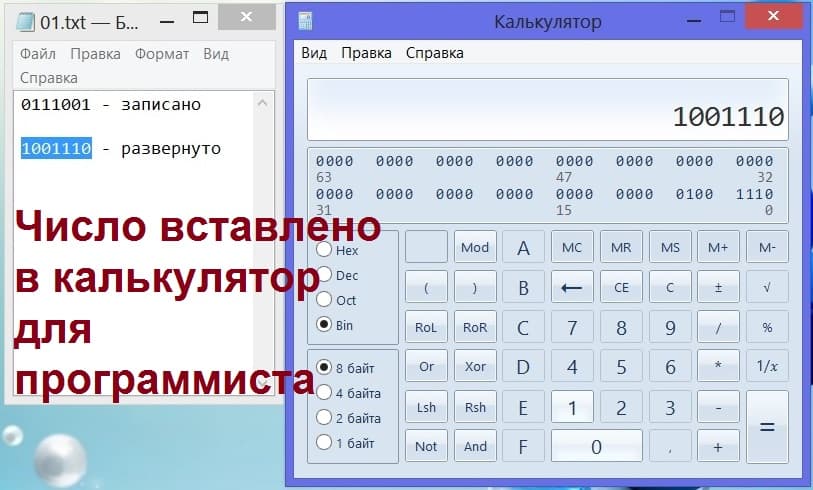
Рис. 15. Вставка двоичного числа на калькуляторе для программиста.
Хорошо! И зачем все это, спросит пытливый читатель? Для того чтобы угадать число! Ведь у нас, как это ни странно, в виде единичек и нулей записано… (Вы не поверите!) то самое загаданное число!!! Но на калькуляторе оно сейчас выглядит непонятно, в двоичном виде.
Давайте превратим 1001110 в десятичное число. Для этого на калькуляторе желательно сначала нажать на знак равенства «=», чтобы число «зафиксировать». А затем потребуется сменить настройки калькулятора для программиста. Нажмем на кнопку настроек «Dec», что означает «десятичное число» (рис. 16).
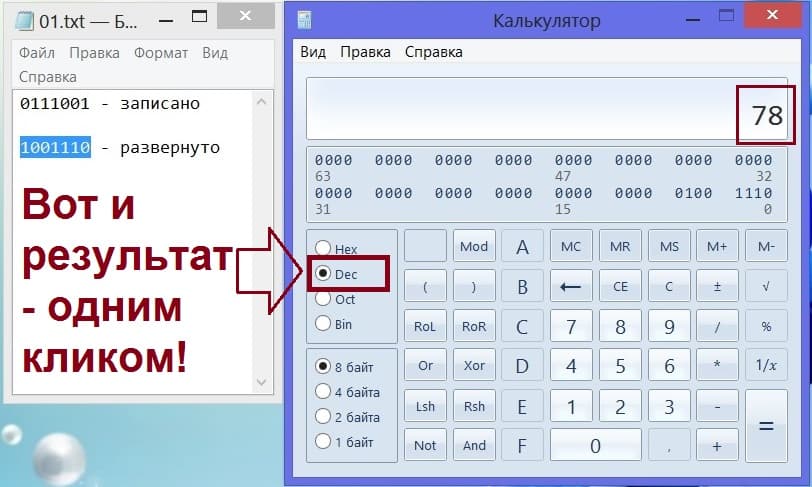
Рис. 16. Переключение калькулятора для программиста в режим работы с десятичными числами – это сразу же дает нам конечный результат, задуманное десятичное число.
Вот и результат – прямо на экране того же калькулятора. Это и есть то самое число, которое было загадано: 78!
Видео: Угадай задуманное число
Фокусы должны быть с разоблачениями
Классик требовал разоблачения фокусов (М.Булгаков «Мастер и Маргарита»). Нам тоже надо бы объяснить, как мы получили результат. Как получилось, что удалось столь просто воспроизвести задуманное число? Хорошо, постараемся…
Наш партнер постоянно делил числа пополам. И отбрасывал дробную часть. Иными словами – наш партнер делил число «нацело без остатка». Единственное, что он нам сообщал – это величина остатка от деления числа нацело.
В остатке от деления на 2 мог быть либо ноль, либо могла быть единица, и больше ничего другого. А ведь именно так десятичное число превращается в двоичное! Двоичное число записывается в виде последовательности нулей и единиц, которые остаются в остатке при делении на 2 нацело.
Выходит, что наш товарищ нам просто сообщал о своем числе, но только не в десятичном формате, а в двоичном формате. Он нам так прямо и говорил в ходе игры: «я задумал(а) число 1001110». Правда, сделано это было в неявном виде, именно так и устроены числовые фокусы.
Как преобразовать двоичное число в десятичное
Нам же осталось только преобразовать двоичное число в десятичное, как только мы узнали, что задуманное число есть 1001110. Это было сделано с помощью калькулятора для программиста – ввод двоичного числа с получением взамен десятичного.
А можно ли «вручную» преобразовать двоичное число в десятичное? Конечно. Для этого нужно каждую единичку умножить на соответствующий разряд этого двоичного числа. А потом все цифры сложить. Если не ошибиться при работе «руками», то результат непременно получится 78.
На рисунке 17 продемонстрировано, как мы в игровой форме преобразовывали десятичное число сначала в двоичное, а потом наоборот. Каждое деление нацело на 2 давало нам в остатке 0 или 1. Из этих «нулей» и «единиц» мы формировали и записали двоичное число 1001110. А затем произвели обратное преобразование в десятичный вид путем умножения с последующим сложением:
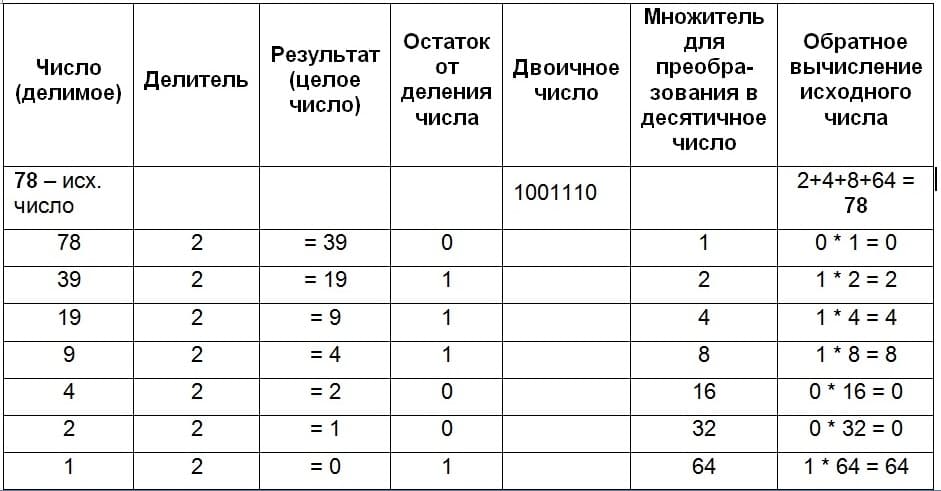
Рис 17 (Кликните для увеличения). Таблица, демонстрирующая вычисления для преобразования задуманного десятичного числа в двоичное, и затем – наоборот.
Приведенный рисунок наглядно показывает нам, как преобразуется десятичное число в двоичное: путем последовательного деления на 2. Наоборот, двоичное число превращается в десятичное число с помощью умножения каждого нолика и единички на такие числа, как 1, 2, 4, 8, 16, 32, 64, 128, … После чего все числа складывают и получают требуемый результат.
Вот так можно использовать наши знания двоичной системы исчисления для небольшого приятного фокуса «Угадай число!».
О возможной пользе троичной, четверичной и иных систем счисления
Кстати, аналогично можно преобразовать десятичное число в троичное. Только придется делить нацело не на 2, а на 3. Тоже потребуется записывать цифры из остатка, которые могут быть 0, 1 и 2. Для перевода в четверичную систему делить уже придется на 4, а в остатке записывать цифры 0, 1, 2, 3. И так далее – для любой системы исчисления правила однотипные, только делить приходится на разные числа.
А как потом преобразовать троичное или четверичное число в десятичное? На какие множители придется умножать цифры 0, 1, 2 и 0, 1, 2 и 3 соответственно? Как Вы думаете?! Делаем паузу, чтобы можно было подумать самостоятельно…
- …В двоичной системе – то были цифры 1, 2, 4, 8 и так далее – каждое последующее число есть предыдущее, умноженное на 2.
- А в троичной же системе это будут цифры 1, 3, 9, 27 и так далее – каждое последующее число есть умножение на 3.
- В четверичной системе: 1, 4, 16, 64 и так далее – теперь умножаем каждое число на 4!
Можете теперь самостоятельно записать аналогичные числа в пятеричной системе?! А в шестеричной?..
Вот так, довольно просто и единообразно можно преобразовывать числа из десятичной системы счисления в любые другие системы. Зачем? Например, показывать фокусы!
О системах счисления в технике
В технике тоже нужны иные системы счисления. Допустим, по проводу может протекать ток. Если по нему либо есть ток, либо нет – это двоичная система. А если по проводу ток может течь в два направления «+» и «-», то тут мы имеем дело с троичной системой: «-» (ток течет в обратном направлении), «0» (нет тока), «+» (ток течет в прямом направлении). Придется рассчитывать подобные цепи с применением троичной системы исчисления.
Или, скажем, если нам придется пользоваться старинными весами с двумя чашками, куда и слева, и справа можно ставить разные гирьки. Тогда, как оказывается, самые универсальные разновесы с наименьшим числом гирек получаются, если они будут сделаны не в привычной двоичной системе (1, 2, 4, 8 и так далее), а в троичной системе (1, 3, 9, 27 и так далее).
Но эти гирьки 1, 3, 9, 27, или ток, текущий в разных направлениях, что называется, уже совсем другая история…
Другие материалы:
1. Кодирование текстовой информации
3. Сказка про мудрого правителя Процессора, про злого Вируса и неутомимого Анти Вируса
4. Игра Крестики-нолики онлайн в Google и в браузере Google Chrome
